Projet de classe préparatoire

Notions de base sur les ensembles

Commençons par la définition formelle d’un ensemble. Un ensemble est une collection d’objets distincts, appelés éléments, qui peuvent satisfaire certaines propriétés. Par exemple, l’ensemble des nombres pairs pourrait être représenté comme {2, 4, 6, 8, …}. Chaque nombre dans cet ensemble est un élément.

La notation standard pour représenter les ensembles utilise des accolades {}. Pour indiquer qu’un élément appartient à un ensemble, nous utilisons le symbole « ∈ ». Par exemple, pour dire que le nombre 4 appartient à l’ensemble des nombres pairs, nous écrivons 4 ∈ {2, 4, 6, 8, …}. De même, si un élément n’appartient pas à un ensemble, nous utilisons le symbole « ∉ ».

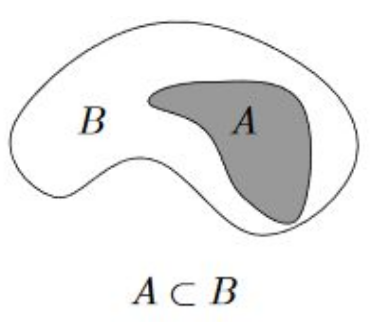
L’ordre des éléments dans un ensemble n’a pas d’importance. {2, 4, 6} est le même ensemble que {4, 2, 6} ou {6, 4, 2}. De plus, les éléments d’un ensemble doivent être uniques ; un élément ne peut apparaître qu’une seule fois.

Opérations sur les ensembles

Les opérations sur les ensembles nous permettent de combiner et de manipuler des ensembles pour en créer de nouveaux. Voici quelques opérations de base :

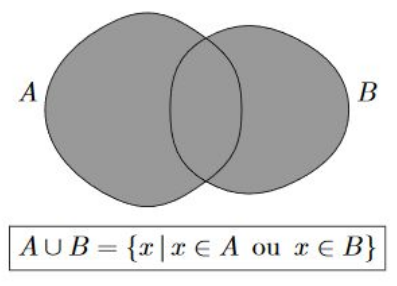
• Union : L’union de deux ensembles, A et B, notée A ∪ B, est un ensemble contenant tous les éléments de A et de B. Par exemple, si A = {1, 2, 3} et B = {2, 4, 6}, alors A ∪ B = {1, 2, 3, 4, 6}.
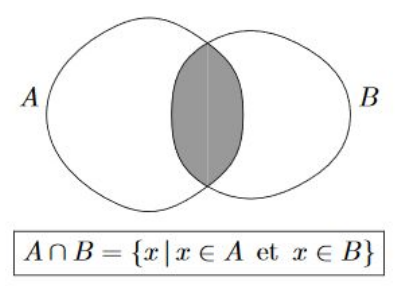
• Intersection : L’intersection de deux ensembles, A et B, notée A ∩ B, est un ensemble contenant les éléments communs à A et B. Dans notre exemple, A ∩ B = {2}.
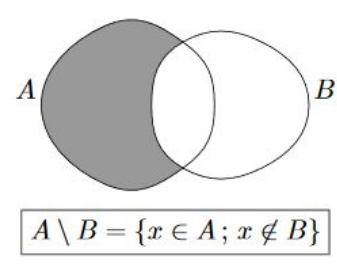
• Différence : La différence entre deux ensembles, A et B, notée A \ B, est un ensemble contenant les éléments de A qui ne sont pas dans B. Ainsi, A \ B = {1, 3} dans notre cas.
• Différence symétrique : La différence symétrique de deux ensembles, A et B, notée A ∆ B, est un ensemble contenant les éléments qui sont dans A ou B, mais pas dans leur intersection. Dans notre exemple, A ∆ B = {1, 3, 4, 6}.
• Complémentaire : Le complémentaire d’un ensemble A, noté A’, est l’ensemble de tous les éléments qui ne sont pas dans A.

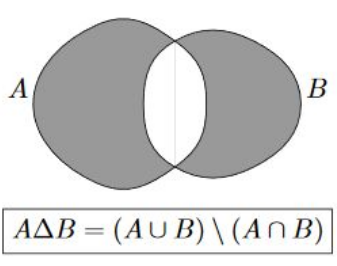
Cardinal de l’ensemble des parties

Le cardinal d’un ensemble, noté card(A), représente le nombre d’éléments distincts dans l’ensemble A. Par exemple, card({1, 2, 3}) = 3. Cependant, le cardinal de l’ensemble des parties d’un ensemble est beaucoup plus intéressant.

Le cardinal de l’ensemble des parties d’un ensemble A, noté P(A), est égal à 2^n, où n est le cardinal de A. Par exemple, si A = {1, 2}, alors P(A) = {{}, {1}, {2}, {1, 2}}. Dans ce cas, card(P(A)) = 2^2 = 4.

Le principe du dénombrement est une application pratique du cardinal de l’ensemble des parties. Il permet de calculer le nombre de résultats possibles lors de plusieurs expériences. Par exemple, si vous lancez deux dés, le nombre de résultats possibles est 6 x 6 = 36, car chaque dé a 6 faces.

Exemples

Considérons les ensembles A = {0, 1, 2, 3} et B = {-1, 2, 3, 10, 55}. Nous pouvons maintenant explorer les opérations sur ces ensembles :

• Intersection : A ∩ B = {2, 3}
• Union : A ∪ B = {-1, 0, 1, 2, 3, 10, 55}
• Cardinal : card(A) = 4 et card(B) = 5

De plus, le cardinal de l’ensemble des parties de A est P(A) = 2^4 = 16, tandis que P(B) = 2^5 = 32.

Conclusion

Les ensembles et les opérations sur les ensembles constituent les fondements des mathématiques. Ils nous permettent de manipuler et de comprendre les collections d’objets, et forment la base de concepts plus avancés en mathématiques et en informatique. En continuant à explorer cette page web, vous découvrirez comment ces concepts s’intègrent dans la théorie des graphes et l’algorithme de Dijkstra.

Les débuts de la théorie des graphes

La théorie des graphes a vu le jour en 1735, lorsque le mathématicien suisse Leonhard Euler a présenté un article à l’Académie de Saint-Pétersbourg. Cet article, publié plus tard en 1741, portait sur un problème intriguant dans la ville de Königsberg (actuellement Kaliningrad, en Russie).

Königsberg était traversée par deux rivières, avec une île au centre nommée Kneiphof. La ville était reliée par sept ponts, comme illustré dans le plan ci-dessous :

Le problème consistait à déterminer s’il était possible de faire une promenade à travers la ville en traversant chaque pont une fois et seulement une fois, et en revenant au point de départ. Euler a simplifié ce problème en représentant la ville sous la forme d’un graphe, avec les rives comme sommets et les ponts comme arêtes.

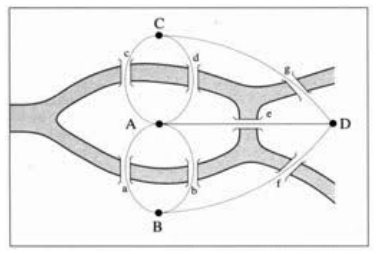
Euler a constaté que chaque sommet (rive) avait un nombre impair d’arêtes (ponts). Il a alors démontré qu’il était impossible de faire une promenade satisfaisant les conditions données, car pour revenir au point de départ, chaque sommet devrait avoir un nombre pair d’arêtes.

Progrès et applications

Au fil du temps, la théorie des graphes a évolué et a trouvé de nombreuses applications dans divers domaines. Au 19e siècle, le mathématicien Arthur Cayley s’est intéressé aux arbres, un type particulier de graphe. Ses travaux ont contribué à approfondir la compréhension des graphes et de leurs propriétés.

La théorie des graphes a également eu un impact significatif sur les probabilités, avec des concepts tels que les marches aléatoires, qui sont à la base du fonctionnement des bourses. De plus, les arbres de probabilité pondérés sont une autre application pratique de la théorie des graphes.

Une application courante de la théorie des graphes que nous rencontrons quotidiennement est la planification d’itinéraires. Les systèmes d’itinéraires et les applications de navigation GPS utilisent des algorithmes basés sur la théorie des graphes pour calculer le chemin le plus court ou le plus rapide entre deux points. Ces algorithmes prennent en compte divers facteurs, tels que la distance, le temps ou la consommation de carburant.

Algorithmes de graphes

Il existe plusieurs algorithmes importants dans la théorie des graphes qui ont des applications pratiques. Voici quelques exemples :

• Algorithme de Welsh-Powell : Cet algorithme permet de colorer les sommets d’un graphe de telle sorte que les sommets adjacents n’aient pas la même couleur. Il est utilisé dans l’attribution de fréquences en télécommunications pour éviter les interférences.
• Algorithme de Dijkstra : Cet algorithme trouve le chemin le plus court entre deux sommets dans un graphe pondéré. Il est couramment utilisé dans la planification d’itinéraires pour déterminer le trajet le plus efficace.
• Algorithme de Bellman-Ford : Cet algorithme calcule le chemin le plus court depuis un sommet initial vers tous les autres sommets dans un graphe pondéré. Il peut gérer des poids d’arêtes négatifs, ce qui n’est pas le cas de l’algorithme de Dijkstra.

Conclusion

La théorie des graphes est une branche des mathématiques à la fois élégante et pratique. Elle trouve ses racines dans un problème du monde réel et a depuis évolué pour avoir un impact significatif sur divers domaines, des mathématiques à l’informatique, en passant par la planification d’itinéraires. En continuant à explorer cette page web, vous découvrirez comment l’algorithme de Dijkstra, l’un des algorithmes les plus connus de la théorie des graphes, est implémenté et utilisé pour résoudre des problèmes concrets.

Présentation de l’algorithme de Dijkstra

L’algorithme de Dijkstra prend en entrée un graphe orienté pondéré par des réels positifs et un sommet source. Son objectif est de déterminer le chemin le plus court depuis le sommet source vers tous les autres sommets du graphe.

L’algorithme fonctionne en construisant progressivement un sous-graphe contenant les sommets classés par ordre croissant de leur distance minimale au sommet source. La distance correspond à la somme des poids des arêtes empruntées.

Au départ, on considère que les distances de chaque sommet au sommet source sont infinies, sauf pour le sommet source lui-même, pour lequel la distance est nulle.

À chaque itération, l’algorithme sélectionne un sommet de distance minimale en dehors du sous-graphe et l’ajoute à celui-ci. Ensuite, il met à jour les distances des sommets voisins du sommet ajouté. La mise à jour consiste à comparer la distance existante avec la somme de la distance du sommet ajouté et du poids de l’arête qui les relie. La distance la plus courte est retenue.

Ce processus se poursuit jusqu’à ce que tous les sommets aient été ajoutés au sous-graphe, ou jusqu’à ce que le sommet d’arrivée soit atteint.

Implémentation de l’algorithme

Pour illustrer l’algorithme de Dijkstra en action, considérons l’exemple suivant :

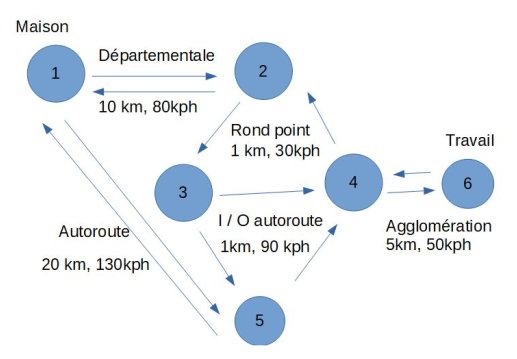
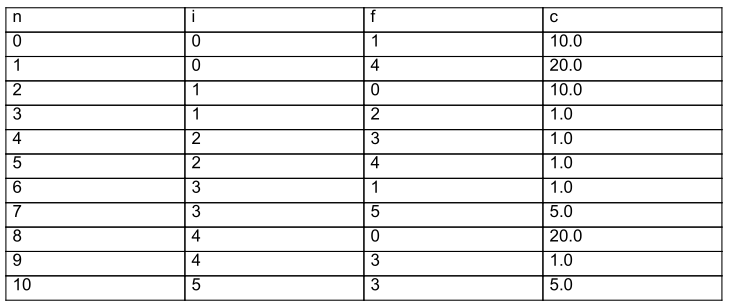
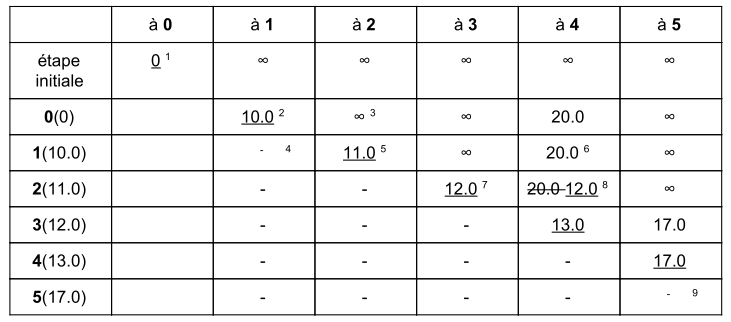
Supposons que nous voulions trouver le chemin le plus court depuis le sommet 0 vers le sommet 5. Voici comment l’algorithme de Dijkstra procéderait :

• Étape 1 : Initialisation. Les distances initiales sont infinies pour tous les sommets, sauf pour le sommet 0, qui a une distance de 0.
• Étape 2 : Sélection du sommet de distance minimale. Le sommet 1 est sélectionné car il a la distance minimale (10.0) parmi les sommets restants.
• Étape 3 : Mise à jour des distances. Les distances des sommets voisins du sommet 1 sont mises à jour. La distance du sommet 2 est mise à jour à 11.0, et la distance du sommet 4 est mise à jour à 20.0.
• Étape 4 : Répétition. L’algorithme continue en sélectionnant le sommet de distance minimale parmi les sommets restants et en mettant à jour les distances des sommets voisins.
• Étape 5 : Arrivée au sommet cible. L’algorithme s’arrête lorsque le sommet cible (5) est atteint. Le chemin le plus court de 0 à 5 est 0-1-2-3-5, avec une distance totale de 17.0.

Implémentation pratique

L’implémentation de l’algorithme de Dijkstra dans un langage de programmation, tel que Processing, permet une utilisation plus efficace. L’idée est de fournir un tableau contenant les chemins possibles, et le programme calcule le chemin le plus court.

L’implémentation implique plusieurs étapes :

1. Utilisation des fonctions implémentées en TP (travaux pratiques) pour gérer les matrices d’adjacence et de transitivité.
2. Implémentation de l’algorithme de Dijkstra pour retourner un tableau contenant le prédécesseur de chaque sommet. Ce tableau est ensuite utilisé pour afficher le chemin le plus court.
3. Implémentation de l’écriture et de la lecture de matrices dans des fichiers, permettant une manipulation aisée de plusieurs graphes.
4. Création d’une interface graphique conviviale, avec un menu permettant de créer de nouveaux graphes, de lire des graphes existants, de voir la licence et de quitter l’application.

Difficultés et solutions

Lors de l’implémentation, certaines difficultés ont été rencontrées et résolues de la manière suivante :

1. La notion de distance infinie : Processing n’a pas de fonction « infini », alors nous avons considéré une valeur très élevée (un milliard) comme infinie.
2. Perte de données : Une perte de données inattendue a été résolue en utilisant l’outil « git » pour créer des sauvegardes du programme et permettre une réversion facile en cas de problèmes.
3. Boucle de traitement des sommets : Une compréhension insuffisante de l’algorithme a initialement causé des problèmes, mais une étude plus approfondie a permis de résoudre cette difficulté.

Conclusion

L’algorithme de Dijkstra est un outil puissant pour trouver le chemin le plus court dans un graphe pondéré. Son implémentation pratique permet une utilisation efficace pour résoudre des problèmes concrets. En explorant cette page web, vous avez découvert comment l’algorithme fonctionne et comment il peut être appliqué pour trouver le chemin le plus court entre deux sommets. N’hésitez pas à expérimenter avec différents graphes et à découvrir d’autres applications de cet algorithme fascinant.